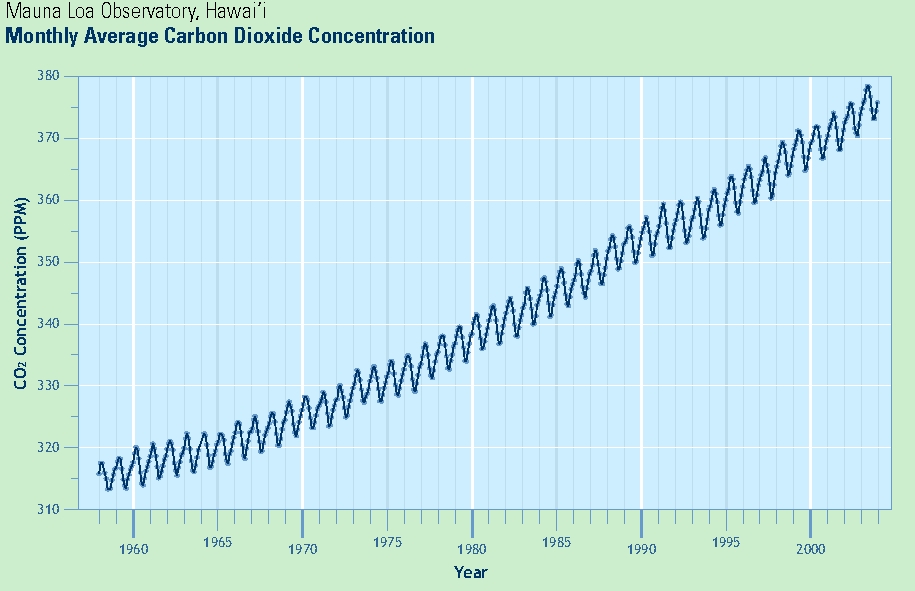
In this exploration you will use slopes of lines to estimate the average rate of change — here, an average rate of increase — of some quantity (in this case, average atmospheric concentrations of CO2 near the Manua Loa Observatory (MLO)) during a time interval.

I. Slopes: Visual/Graphical Approach

1. Using a pencil, mark a point on the graph above the year 1960 at a "middle height" location amidst the zig-zagging line, not at the top nor at the bottom (in particular, it's ok if your point is not exactly on the zig-zagging line itself). Call this point A. Do the same for 1970, 1980, 1990, and 2000 (points B, C, D, and E, respectively).
2. Use a ruler (or another object which can serve as a sufficiently-long straightedge) to draw the line segment between points A and B, and then to carefully continue that line to the right until it reaches the right edge of the above image.
3. Do the same for the line segment between B and C, likewise continuing it to the right (stop at this point; do not use D and E).
4. Summarize below in a clear, precise, full-English sentences a "regular member of the public" could understand, what, in broad terms these lines indicate about CO2 and rates of change. Be precise!

   __________________________________________________________________________________________

   __________________________________________________________________________________________

   __________________________________________________________________________________________

5. Numerical estimates using the graphical approach. Devise a strategy for approximating the slopes of drawn line segments on a graph such as this (hint: think back to "rise over run" and draw some vertical and horizontal lines through points A, B, and C until you find their approximate x- and y-coordinates; use these to est. "rise" and "run")
   1. Estimate the slope of the line segment from A to B: ______ Estimate the slope of the line segment from B to C: ______
   2. What are the units for these quantities? ______per _____.
   3. Estimate the rate of increase of CO2 during the 2000-2005 period: ______ ppm/yr.

II. Slopes: Numerical Approach

The fuller data from the Carbon Dioxide Information Analysis Center (cdiac.ornl.gov) at the Oak Ridge National Laboratory — the primary climate-change data and information analysis center of the U.S. Department of Energy (DOE) — is found on the 3rd page.

1. Use the data for each year (using the right-most "Annual-fit" column) to fill out the table below:

   Year	(Fit) Avg. Annual CO2 level
   1960	316.91 ppm
   1970	325.65 ppm
   1980	338.67 ppm
   1990	354.19 ppm
   2000	369.47 ppm

2. Now use that data to fill out the table below:

   Time period	Change in Avg CO2 per decade
   1960 to 1970	an increase by 8.74 ppm
   1970 to 1980	an increase by 13.02 ppm
   1980 to 1990	an increase by 15.52 ppm
   1990 to 2000	an increase by 15.28 ppm

   
   
   

3. What new information or understanding, if any, have you unearthed by using this numerical approach, that you didn't have from the graphical approaches above?

   __________________________________________________________________________________________

   __________________________________________________________________________________________

4. Explore below why, in general (regardless of whether the application is CO₂ analysis or other quantities) we might miss some information if we rely only on graphs that is on analysis without numerical details? What do we gain by having numerical values, over having only graphs? Explain clearly.

   __________________________________________________________________________________________

   __________________________________________________________________________________________

5. In light of your answer to the preceding question, another question arises. Namely, "why then do we ever bother with graphs at all?" Why not simply always use only tables of exact values? Do graphs have advantages that the numerical tables (by themselves) lack? Your explanation should be precise, but also understandable by (and convincing to) a lay (non-specialist) audience.

   __________________________________________________________________________________________

   __________________________________________________________________________________________

   __________________________________________________________________________________________